Methods and Cosmology¶
When using fruitbat there are different methods and cosmologies built-in from which you can choose. Below is a brief description of how each method is calculated and the parameters for each cosmology.
Methods¶
Currently there are three built-in dispersion measure-redshift relations. In fruitbat these are referred to as ‘methods’. To calculate the look-up tables fruitbat uses the equations described below for each method to calculate the dispersion measre (\(\rm{DM}\)) for a given redshift (\(z\)).
F(z) Integral¶
The methods 'Ioka2003', 'Inoue2004', 'Zhang2018' all have a common integral \(F(z)\).
Where \(z\) is the redshift, \(\Omega_m\) is the cosmic matter density, \(\Omega_{\Lambda}\) is cosmic dark energy density and \(w\) characterises the dark energy equation of state. This is typically assumed to have a constant value of \(\sim 1.06\) which introduces an error of approximately 6% for \(z < 2\).
The lookup tables in fruitbat explicitly solve this integral for each redshift to when calculating a dispersion measure. See the Figure below for a comparison between the assumed value and the integral in fruitbat.

Ioka 2003¶
The Ioka (2003) method assumes that all baryons in the Universe are fully ionised and that there is a 1-to-1 relation between eletrons and baryons. i.e. The number is free electrons in the Universe is the same as the number of baryons. The DM at a given redshift using the Ioka method is calculated as follows:
Where \(c\) is the speed of light, \(H_0\) is the Hubble constant, \(\Omega_b\) is the cosmic baryon density, \(G\) is the gravitational constant, \(m_p\) is the mass of the proton and \(F(z)\) is the integral defined earlier.
Inoue 2004¶
The Inoue (2004) method assumes that hydrogen is fully ionised and helium is singly ionised. THe DM at a given redshift using the Inoue method is calculated as follows.
Where \(c\) is the speed of light, \(H_0\) is the Hubble constant, \(\Omega_b\) is the cosmic baryon density and \(F(z)\) is the integral defined earlier. The factor of \(9.2 \times 10^{-10}\) comes estimating the number of free electrons at high redshifts from models of reionisation.
Zhang 2018¶
The Zhang (2018) method assumes that all baryons in the Universe are fully ionised and that there is a 0.875-to-1 ratio between eletrons and baryons, and that 85% of baryons are in the intergalactic medium. The DM at a given redshift using the Zhang method is calculated as follows:
Where \(c\) is the speed of light, \(H_0\) is the Hubble constant, \(\Omega_b\) is the cosmic baryon density, \(G\) is the gravitational constant, \(m_p\) is the mass of the proton, \(\chi\) is the free electron per baryon in the Universe, \(f_{igm}\) is the fraction of baryons in the intergalactic medium and \(F(z)\) is the integral defined earlier.
\(\chi\) is calculated as follows:
Where \(\chi_{e, H}\) and \(\chi_{e, He}\) denote the ionisation fraction of hydrogen and helium respectively and \(y_1 \sim y_2 \sim 1\) denote the possible slight deviation from the 3/4 - 1/4 split of hydrogen and helium abundance in the Universe. Assuming that hydrogen and helium are both ionised, then \(\chi(z) \sim 0.875\).
Cosmology¶
Each method in fruitbat has a list of pre-calculated lookup tables with different cosmologies. The table below lists the parameters that are used for each cosmology.
| Cosmological Parameters | |||||
|---|---|---|---|---|---|
| Keyword | \(H_0\) | \(\Omega_b\) | \(\Omega_m\) | \(\Omega_\Lambda\) | \(w\) |
'WMAP5' |
\(70.2\) | \(0.0459\) | \(0.277\) | \(0.723\) | -1 |
'WMAP7' |
\(70.4\) | \(0.0455\) | \(0.272\) | \(0.728\) | -1 |
'WMAP9' |
\(69.32\) | \(0.04628\) | \(0.2865\) | \(0.7134\) | -1 |
'Planck13' |
\(67.77\) | \(0.0483\) | \(0.3071\) | \(0.6914\) | -1 |
'Planck15' |
\(67.74\) | \(0.0486\) | \(0.3075\) | \(0.6910\) | -1 |
'Planck18' |
\(67.66\) | \(0.04897\) | \(0.3111\) | \(0.6874\) | -1 |
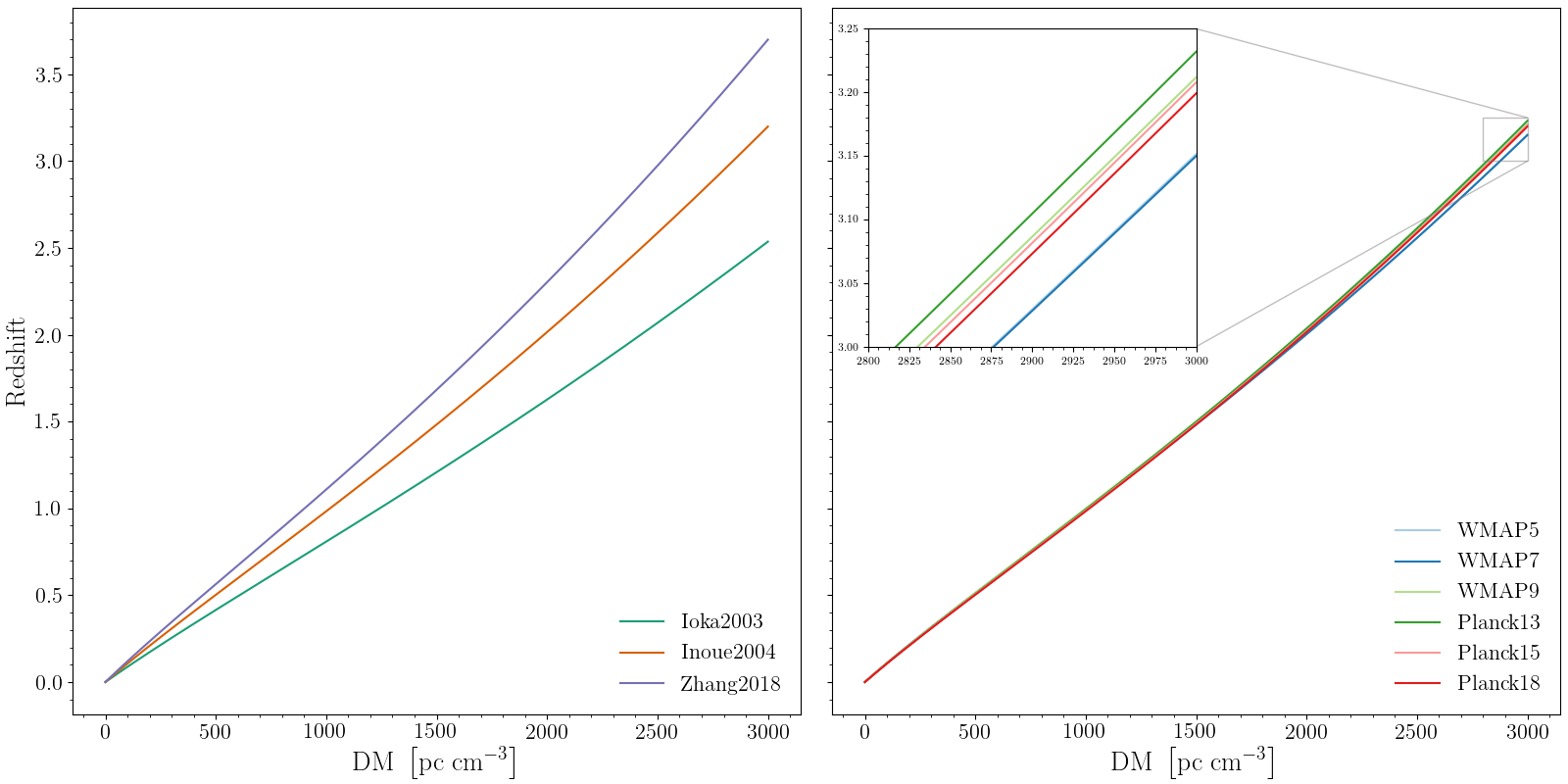
Below is a figure comparing the different methods and cosmologies in fruitbat. The left figure shows how the different methods compare assuming a 'Planck18' cosmology..
The right figure shows how the 'Inoue2004' method changes with different assumed cosmologies.